Forecasting I: univariate, heavy tailed¶
This tutorial introduces the pyro.contrib.forecast module, a framework for forecasting with Pyro models. This tutorial covers only univariate models and simple likelihoods. This tutorial assumes the reader is already familiar with SVI and tensor shapes.
See also:
Summary¶
To create a forecasting model:
Create a subclass of the ForecastingModel class.
Implement the .model(zero_data, covariates) method using standard Pyro syntax.
Sample all time-local variables inside the self.time_plate context.
Finally call the .predict(noise_dist, prediction) method.
To train a forecasting model, create a Forecaster object.
Training can be flaky, you’ll need to tune hyperparameters and randomly restart.
Reparameterization can help learning, e.g. LocScaleReparam.
To forecast the future, draw samples from a
Forecasterobject conditioned on data and covariates.To model seasonality, use helpers periodic_features(), periodic_repeat(), and periodic_cumsum().
To model heavy-tailed data, use Stable distributions and StableReparam.
To evaluate results, use the backtest() helper or low-level loss functions.
[1]:
import torch
import pyro
import pyro.distributions as dist
import pyro.poutine as poutine
from pyro.contrib.examples.bart import load_bart_od
from pyro.contrib.forecast import ForecastingModel, Forecaster, backtest, eval_crps
from pyro.infer.reparam import LocScaleReparam, StableReparam
from pyro.ops.tensor_utils import periodic_cumsum, periodic_repeat, periodic_features
from pyro.ops.stats import quantile
import matplotlib.pyplot as plt
%matplotlib inline
assert pyro.__version__.startswith('1.9.1')
pyro.set_rng_seed(20200221)
[2]:
dataset = load_bart_od()
print(dataset.keys())
print(dataset["counts"].shape)
print(" ".join(dataset["stations"]))
dict_keys(['stations', 'start_date', 'counts'])
torch.Size([78888, 50, 50])
12TH 16TH 19TH 24TH ANTC ASHB BALB BAYF BERY CAST CIVC COLM COLS CONC DALY DBRK DELN DUBL EMBR FRMT FTVL GLEN HAYW LAFY LAKE MCAR MLBR MLPT MONT NBRK NCON OAKL ORIN PCTR PHIL PITT PLZA POWL RICH ROCK SANL SBRN SFIA SHAY SSAN UCTY WARM WCRK WDUB WOAK
Intro to Pyro’s forecasting framework¶
Pyro’s forecasting framework consists of: - a ForecastingModel base class, whose .model() method can be implemented for custom forecasting models, - a Forecaster class that trains and forecasts using ForecastingModels, and - a
backtest() helper to evaluate models on a number of metrics.
Consider a simple univariate dataset, say weekly BART train ridership aggregated over all stations in the network. This data roughly logarithmic, so we log-transform for modeling.
[3]:
T, O, D = dataset["counts"].shape
data = dataset["counts"][:T // (24 * 7) * 24 * 7].reshape(T // (24 * 7), -1).sum(-1).log()
data = data.unsqueeze(-1)
plt.figure(figsize=(9, 3))
plt.plot(data)
plt.title("Total weekly ridership")
plt.ylabel("log(# rides)")
plt.xlabel("Week after 2011-01-01")
plt.xlim(0, len(data));
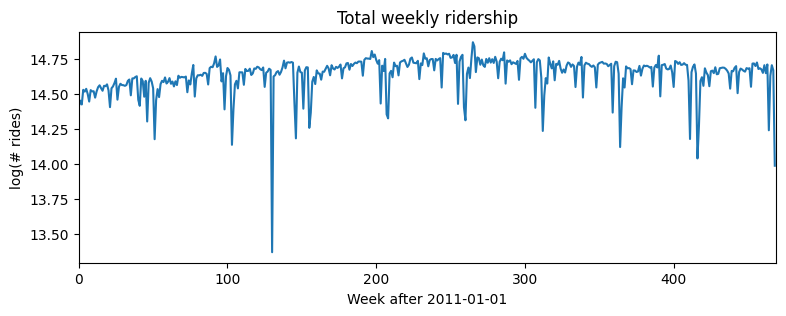
Let’s start with a simple log-linear regression model, with no trend or seasonality. Note that while this example is univariate, Pyro’s forecasting framework is multivariate, so we’ll often need to reshape using .unsqueeze(-1), .expand([1]), and .to_event(1).
[4]:
# First we need some boilerplate to create a class and define a .model() method.
class Model1(ForecastingModel):
# We then implement the .model() method. Since this is a generative model, it shouldn't
# look at data; however it is convenient to see the shape of data we're supposed to
# generate, so this inputs a zeros_like(data) tensor instead of the actual data.
def model(self, zero_data, covariates):
data_dim = zero_data.size(-1) # Should be 1 in this univariate tutorial.
feature_dim = covariates.size(-1)
# The first part of the model is a probabilistic program to create a prediction.
# We use the zero_data as a template for the shape of the prediction.
bias = pyro.sample("bias", dist.Normal(0, 10).expand([data_dim]).to_event(1))
weight = pyro.sample("weight", dist.Normal(0, 0.1).expand([feature_dim]).to_event(1))
prediction = bias + (weight * covariates).sum(-1, keepdim=True)
# The prediction should have the same shape as zero_data (duration, obs_dim),
# but may have additional sample dimensions on the left.
assert prediction.shape[-2:] == zero_data.shape
# The next part of the model creates a likelihood or noise distribution.
# Again we'll be Bayesian and write this as a probabilistic program with
# priors over parameters.
noise_scale = pyro.sample("noise_scale", dist.LogNormal(-5, 5).expand([1]).to_event(1))
noise_dist = dist.Normal(0, noise_scale)
# The final step is to call the .predict() method.
self.predict(noise_dist, prediction)
We can now train this model by creating a Forecaster object. We’ll split the data into [T0,T1) for training and [T1,T2) for testing.
[5]:
T0 = 0 # begining
T2 = data.size(-2) # end
T1 = T2 - 52 # train/test split
[6]:
%%time
pyro.set_rng_seed(1)
pyro.clear_param_store()
time = torch.arange(float(T2)) / 365
covariates = torch.stack([time], dim=-1)
forecaster = Forecaster(Model1(), data[:T1], covariates[:T1], learning_rate=0.1)
INFO step 0 loss = 484401
INFO step 100 loss = 0.609042
INFO step 200 loss = -0.535144
INFO step 300 loss = -0.605789
INFO step 400 loss = -0.59744
INFO step 500 loss = -0.596203
INFO step 600 loss = -0.614217
INFO step 700 loss = -0.612415
INFO step 800 loss = -0.613236
INFO step 900 loss = -0.59879
INFO step 1000 loss = -0.601271
CPU times: user 4.37 s, sys: 30.4 ms, total: 4.4 s
Wall time: 4.4 s
Next we can evaluate by drawing posterior samples from the forecaster, passing in full covariates but only partial data. We’ll use Pyro’s quantile() function to plot median and an 80% confidence interval. To evaluate fit we’ll use eval_crps() to compute Continuous Ranked Probability Score; this is an good metric to assess distributional fit of a heavy-tailed distribution.
[7]:
samples = forecaster(data[:T1], covariates, num_samples=1000)
p10, p50, p90 = quantile(samples, (0.1, 0.5, 0.9)).squeeze(-1)
crps = eval_crps(samples, data[T1:])
print(samples.shape, p10.shape)
plt.figure(figsize=(9, 3))
plt.fill_between(torch.arange(T1, T2), p10, p90, color="red", alpha=0.3)
plt.plot(torch.arange(T1, T2), p50, 'r-', label='forecast')
plt.plot(data, 'k-', label='truth')
plt.title("Total weekly ridership (CRPS = {:0.3g})".format(crps))
plt.ylabel("log(# rides)")
plt.xlabel("Week after 2011-01-01")
plt.xlim(0, None)
plt.legend(loc="best");
torch.Size([1000, 52, 1]) torch.Size([52])
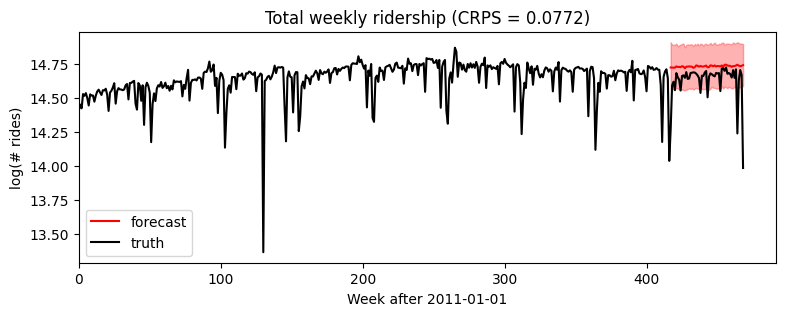
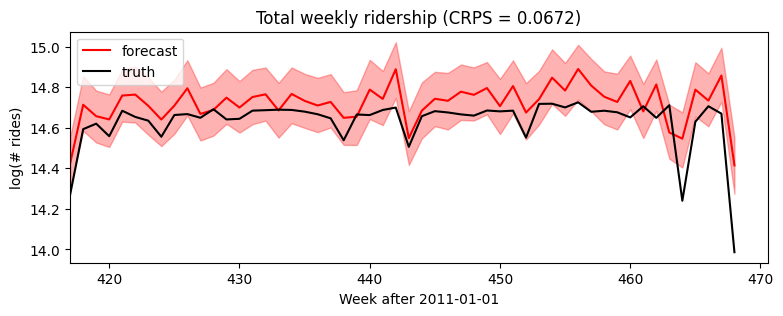
Zooming in to just the forecasted region, we see this model ignores seasonal behavior.
[8]:
plt.figure(figsize=(9, 3))
plt.fill_between(torch.arange(T1, T2), p10, p90, color="red", alpha=0.3)
plt.plot(torch.arange(T1, T2), p50, 'r-', label='forecast')
plt.plot(torch.arange(T1, T2), data[T1:], 'k-', label='truth')
plt.title("Total weekly ridership (CRPS = {:0.3g})".format(crps))
plt.ylabel("log(# rides)")
plt.xlabel("Week after 2011-01-01")
plt.xlim(T1, None)
plt.legend(loc="best");
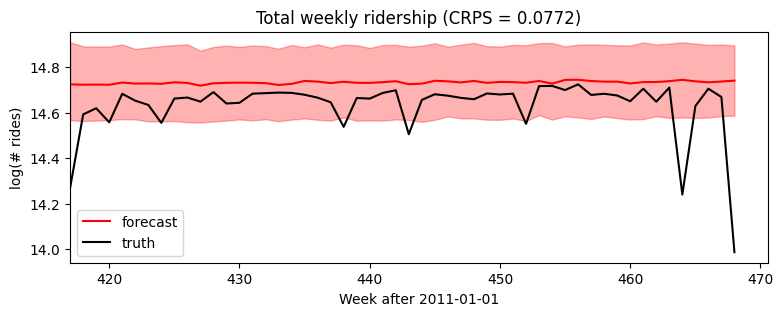
We could add a yearly seasonal component simply by adding new covariates (note we’ve already taken care in the model to handle feature_dim > 1).
[9]:
%%time
pyro.set_rng_seed(1)
pyro.clear_param_store()
time = torch.arange(float(T2)) / 365
covariates = torch.cat([time.unsqueeze(-1),
periodic_features(T2, 365.25 / 7)], dim=-1)
forecaster = Forecaster(Model1(), data[:T1], covariates[:T1], learning_rate=0.1)
INFO step 0 loss = 53174.4
INFO step 100 loss = 0.519148
INFO step 200 loss = -0.0264822
INFO step 300 loss = -0.314983
INFO step 400 loss = -0.413243
INFO step 500 loss = -0.487756
INFO step 600 loss = -0.472516
INFO step 700 loss = -0.595866
INFO step 800 loss = -0.500985
INFO step 900 loss = -0.558623
INFO step 1000 loss = -0.589603
CPU times: user 4.5 s, sys: 34.3 ms, total: 4.53 s
Wall time: 4.54 s
[10]:
samples = forecaster(data[:T1], covariates, num_samples=1000)
p10, p50, p90 = quantile(samples, (0.1, 0.5, 0.9)).squeeze(-1)
crps = eval_crps(samples, data[T1:])
plt.figure(figsize=(9, 3))
plt.fill_between(torch.arange(T1, T2), p10, p90, color="red", alpha=0.3)
plt.plot(torch.arange(T1, T2), p50, 'r-', label='forecast')
plt.plot(data, 'k-', label='truth')
plt.title("Total weekly ridership (CRPS = {:0.3g})".format(crps))
plt.ylabel("log(# rides)")
plt.xlabel("Week after 2011-01-01")
plt.xlim(0, None)
plt.legend(loc="best");
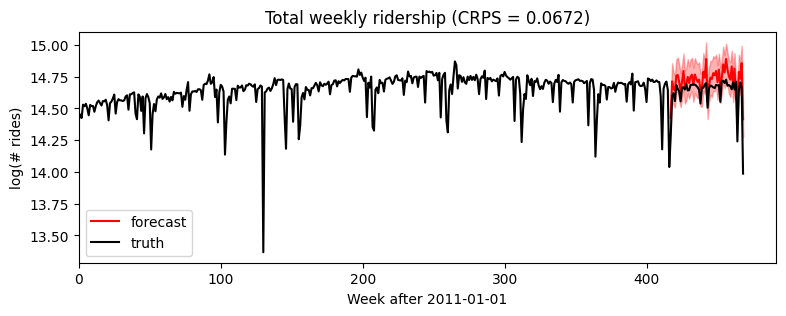
[11]:
plt.figure(figsize=(9, 3))
plt.fill_between(torch.arange(T1, T2), p10, p90, color="red", alpha=0.3)
plt.plot(torch.arange(T1, T2), p50, 'r-', label='forecast')
plt.plot(torch.arange(T1, T2), data[T1:], 'k-', label='truth')
plt.title("Total weekly ridership (CRPS = {:0.3g})".format(crps))
plt.ylabel("log(# rides)")
plt.xlabel("Week after 2011-01-01")
plt.xlim(T1, None)
plt.legend(loc="best");
Time-local random variables: self.time_plate¶
So far we’ve seen the ForecastingModel.model() method and self.predict(). The last piece of forecasting-specific syntax is the self.time_plate context for time-local variables. To see how this works, consider changing our global linear trend model above to a local level model. Note the poutine.reparam() handler is a general Pyro inference trick, not specific to forecasting.
[12]:
class Model2(ForecastingModel):
def model(self, zero_data, covariates):
data_dim = zero_data.size(-1)
feature_dim = covariates.size(-1)
bias = pyro.sample("bias", dist.Normal(0, 10).expand([data_dim]).to_event(1))
weight = pyro.sample("weight", dist.Normal(0, 0.1).expand([feature_dim]).to_event(1))
# We'll sample a time-global scale parameter outside the time plate,
# then time-local iid noise inside the time plate.
drift_scale = pyro.sample("drift_scale",
dist.LogNormal(-20, 5).expand([1]).to_event(1))
with self.time_plate:
# We'll use a reparameterizer to improve variational fit. The model would still be
# correct if you removed this context manager, but the fit appears to be worse.
with poutine.reparam(config={"drift": LocScaleReparam()}):
drift = pyro.sample("drift", dist.Normal(zero_data, drift_scale).to_event(1))
# After we sample the iid "drift" noise we can combine it in any time-dependent way.
# It is important to keep everything inside the plate independent and apply dependent
# transforms outside the plate.
motion = drift.cumsum(-2) # A Brownian motion.
# The prediction now includes three terms.
prediction = motion + bias + (weight * covariates).sum(-1, keepdim=True)
assert prediction.shape[-2:] == zero_data.shape
# Construct the noise distribution and predict.
noise_scale = pyro.sample("noise_scale", dist.LogNormal(-5, 5).expand([1]).to_event(1))
noise_dist = dist.Normal(0, noise_scale)
self.predict(noise_dist, prediction)
[13]:
%%time
pyro.set_rng_seed(1)
pyro.clear_param_store()
time = torch.arange(float(T2)) / 365
covariates = periodic_features(T2, 365.25 / 7)
forecaster = Forecaster(Model2(), data[:T1], covariates[:T1], learning_rate=0.1,
time_reparam="dct",
)
INFO step 0 loss = 1.73259e+09
INFO step 100 loss = 0.935019
INFO step 200 loss = -0.0290582
INFO step 300 loss = -0.193718
INFO step 400 loss = -0.292689
INFO step 500 loss = -0.411964
INFO step 600 loss = -0.291355
INFO step 700 loss = -0.414344
INFO step 800 loss = -0.472016
INFO step 900 loss = -0.480997
INFO step 1000 loss = -0.540629
CPU times: user 9.47 s, sys: 56.4 ms, total: 9.52 s
Wall time: 9.54 s
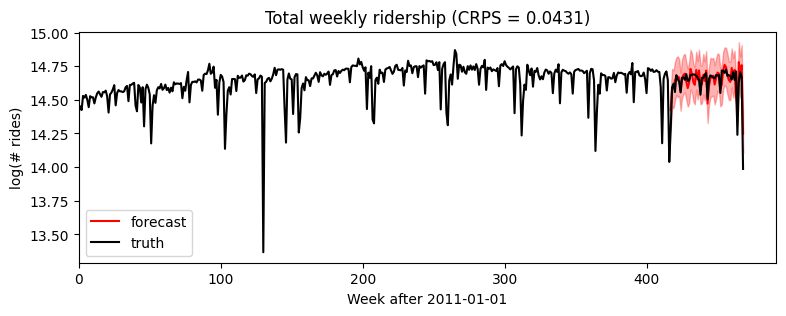
[14]:
samples = forecaster(data[:T1], covariates, num_samples=1000)
p10, p50, p90 = quantile(samples, (0.1, 0.5, 0.9)).squeeze(-1)
crps = eval_crps(samples, data[T1:])
plt.figure(figsize=(9, 3))
plt.fill_between(torch.arange(T1, T2), p10, p90, color="red", alpha=0.3)
plt.plot(torch.arange(T1, T2), p50, 'r-', label='forecast')
plt.plot(data, 'k-', label='truth')
plt.title("Total weekly ridership (CRPS = {:0.3g})".format(crps))
plt.ylabel("log(# rides)")
plt.xlabel("Week after 2011-01-01")
plt.xlim(0, None)
plt.legend(loc="best");
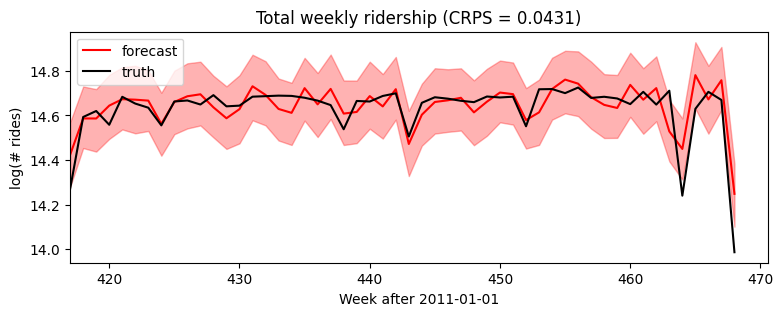
[15]:
plt.figure(figsize=(9, 3))
plt.fill_between(torch.arange(T1, T2), p10, p90, color="red", alpha=0.3)
plt.plot(torch.arange(T1, T2), p50, 'r-', label='forecast')
plt.plot(torch.arange(T1, T2), data[T1:], 'k-', label='truth')
plt.title("Total weekly ridership (CRPS = {:0.3g})".format(crps))
plt.ylabel("log(# rides)")
plt.xlabel("Week after 2011-01-01")
plt.xlim(T1, None)
plt.legend(loc="best");
Heavy-tailed noise¶
Our final univariate model will generalize from Gaussian noise to heavy-tailed Stable noise. The only difference is the noise_dist which now takes two new parameters: stability determines tail weight and skew determines the relative size of positive versus negative spikes.
The Stable distribution is a natural heavy-tailed generalization of the Normal distribution, but it is difficult to work with due to its intractible density function. Pyro implements auxiliary variable methods for working with Stable distributions. To inform Pyro to use those auxiliary variable methods, we wrap the final line in poutine.reparam() effect handler
that applies the StableReparam transform to the implicit observe site named “residual”. You can use Stable distributions for other sites by specifying config={"my_site_name": StableReparam()}.
[16]:
class Model3(ForecastingModel):
def model(self, zero_data, covariates):
data_dim = zero_data.size(-1)
feature_dim = covariates.size(-1)
bias = pyro.sample("bias", dist.Normal(0, 10).expand([data_dim]).to_event(1))
weight = pyro.sample("weight", dist.Normal(0, 0.1).expand([feature_dim]).to_event(1))
drift_scale = pyro.sample("drift_scale", dist.LogNormal(-20, 5).expand([1]).to_event(1))
with self.time_plate:
with poutine.reparam(config={"drift": LocScaleReparam()}):
drift = pyro.sample("drift", dist.Normal(zero_data, drift_scale).to_event(1))
motion = drift.cumsum(-2) # A Brownian motion.
prediction = motion + bias + (weight * covariates).sum(-1, keepdim=True)
assert prediction.shape[-2:] == zero_data.shape
# The next part of the model creates a likelihood or noise distribution.
# Again we'll be Bayesian and write this as a probabilistic program with
# priors over parameters.
stability = pyro.sample("noise_stability", dist.Uniform(1, 2).expand([1]).to_event(1))
skew = pyro.sample("noise_skew", dist.Uniform(-1, 1).expand([1]).to_event(1))
scale = pyro.sample("noise_scale", dist.LogNormal(-5, 5).expand([1]).to_event(1))
noise_dist = dist.Stable(stability, skew, scale)
# We need to use a reparameterizer to handle the Stable distribution.
# Note "residual" is the name of Pyro's internal sample site in self.predict().
with poutine.reparam(config={"residual": StableReparam()}):
self.predict(noise_dist, prediction)
[17]:
%%time
pyro.set_rng_seed(2)
pyro.clear_param_store()
time = torch.arange(float(T2)) / 365
covariates = periodic_features(T2, 365.25 / 7)
forecaster = Forecaster(Model3(), data[:T1], covariates[:T1], learning_rate=0.1,
time_reparam="dct")
for name, value in forecaster.guide.median().items():
if value.numel() == 1:
print("{} = {:0.4g}".format(name, value.item()))
INFO step 0 loss = 5.92061e+07
INFO step 100 loss = 13.6553
INFO step 200 loss = 3.18891
INFO step 300 loss = 0.884046
INFO step 400 loss = 0.27383
INFO step 500 loss = -0.0354842
INFO step 600 loss = -0.211247
INFO step 700 loss = -0.311198
INFO step 800 loss = -0.259799
INFO step 900 loss = -0.326406
INFO step 1000 loss = -0.306335
bias = 14.64
drift_scale = 3.234e-08
noise_stability = 1.937
noise_skew = 0.004095
noise_scale = 0.06038
CPU times: user 19.5 s, sys: 103 ms, total: 19.6 s
Wall time: 19.7 s
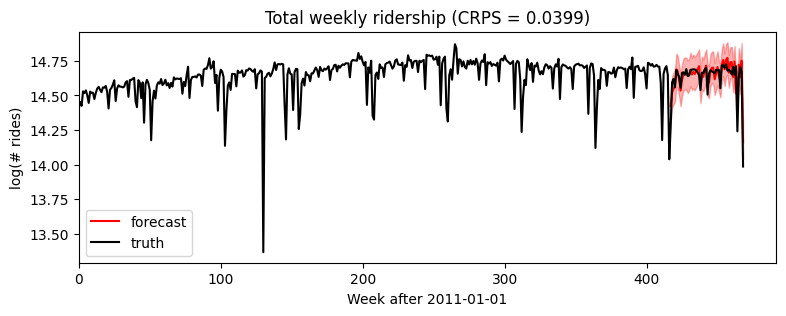
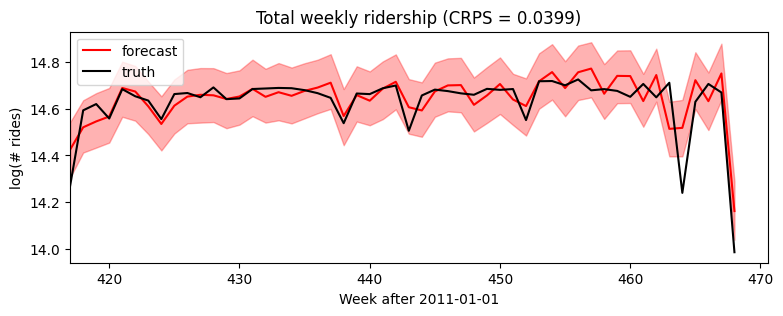
[18]:
samples = forecaster(data[:T1], covariates, num_samples=1000)
p10, p50, p90 = quantile(samples, (0.1, 0.5, 0.9)).squeeze(-1)
crps = eval_crps(samples, data[T1:])
plt.figure(figsize=(9, 3))
plt.fill_between(torch.arange(T1, T2), p10, p90, color="red", alpha=0.3)
plt.plot(torch.arange(T1, T2), p50, 'r-', label='forecast')
plt.plot(data, 'k-', label='truth')
plt.title("Total weekly ridership (CRPS = {:0.3g})".format(crps))
plt.ylabel("log(# rides)")
plt.xlabel("Week after 2011-01-01")
plt.xlim(0, None)
plt.legend(loc="best");
[19]:
plt.figure(figsize=(9, 3))
plt.fill_between(torch.arange(T1, T2), p10, p90, color="red", alpha=0.3)
plt.plot(torch.arange(T1, T2), p50, 'r-', label='forecast')
plt.plot(torch.arange(T1, T2), data[T1:], 'k-', label='truth')
plt.title("Total weekly ridership (CRPS = {:0.3g})".format(crps))
plt.ylabel("log(# rides)")
plt.xlabel("Week after 2011-01-01")
plt.xlim(T1, None)
plt.legend(loc="best");
Backtesting¶
To compare our Gaussian Model2 and Stable Model3 we’ll use a simple backtesting() helper. This helper by default evaluates three metrics: CRPS assesses distributional accuracy of heavy-tailed data,
MAE assesses point accuracy of heavy-tailed data, and RMSE assesses accuracy of Normal-tailed data. The one nuance here is to set warm_start=True to reduce the need for random restarts.
[20]:
%%time
pyro.set_rng_seed(1)
pyro.clear_param_store()
windows2 = backtest(data, covariates, Model2,
min_train_window=104, test_window=52, stride=26,
forecaster_options={"learning_rate": 0.1, "time_reparam": "dct",
"log_every": 1000, "warm_start": True})
INFO Training on window [0:104], testing on window [104:156]
INFO step 0 loss = 3543.21
INFO step 1000 loss = 0.140962
INFO Training on window [0:130], testing on window [130:182]
INFO step 0 loss = 0.27281
INFO step 1000 loss = -0.227765
INFO Training on window [0:156], testing on window [156:208]
INFO step 0 loss = 0.622017
INFO step 1000 loss = -0.0232647
INFO Training on window [0:182], testing on window [182:234]
INFO step 0 loss = 0.181045
INFO step 1000 loss = -0.104492
INFO Training on window [0:208], testing on window [208:260]
INFO step 0 loss = 0.160061
INFO step 1000 loss = -0.184363
INFO Training on window [0:234], testing on window [234:286]
INFO step 0 loss = 0.0414903
INFO step 1000 loss = -0.207943
INFO Training on window [0:260], testing on window [260:312]
INFO step 0 loss = -0.00223408
INFO step 1000 loss = -0.256718
INFO Training on window [0:286], testing on window [286:338]
INFO step 0 loss = -0.0552213
INFO step 1000 loss = -0.277793
INFO Training on window [0:312], testing on window [312:364]
INFO step 0 loss = -0.141342
INFO step 1000 loss = -0.36945
INFO Training on window [0:338], testing on window [338:390]
INFO step 0 loss = -0.148779
INFO step 1000 loss = -0.332914
INFO Training on window [0:364], testing on window [364:416]
INFO step 0 loss = -0.27899
INFO step 1000 loss = -0.462222
INFO Training on window [0:390], testing on window [390:442]
INFO step 0 loss = -0.328539
INFO step 1000 loss = -0.463518
INFO Training on window [0:416], testing on window [416:468]
INFO step 0 loss = -0.400719
INFO step 1000 loss = -0.494253
CPU times: user 1min 57s, sys: 502 ms, total: 1min 57s
Wall time: 1min 57s
[21]:
%%time
pyro.set_rng_seed(1)
pyro.clear_param_store()
windows3 = backtest(data, covariates, Model3,
min_train_window=104, test_window=52, stride=26,
forecaster_options={"learning_rate": 0.1, "time_reparam": "dct",
"log_every": 1000, "warm_start": True})
INFO Training on window [0:104], testing on window [104:156]
INFO step 0 loss = 1852.88
INFO step 1000 loss = 0.533988
INFO Training on window [0:130], testing on window [130:182]
INFO step 0 loss = 2.60906
INFO step 1000 loss = 0.0715323
INFO Training on window [0:156], testing on window [156:208]
INFO step 0 loss = 2.60063
INFO step 1000 loss = 0.110426
INFO Training on window [0:182], testing on window [182:234]
INFO step 0 loss = 1.99784
INFO step 1000 loss = 0.020393
INFO Training on window [0:208], testing on window [208:260]
INFO step 0 loss = 1.63004
INFO step 1000 loss = -0.0936131
INFO Training on window [0:234], testing on window [234:286]
INFO step 0 loss = 1.33227
INFO step 1000 loss = -0.114948
INFO Training on window [0:260], testing on window [260:312]
INFO step 0 loss = 1.19163
INFO step 1000 loss = -0.193086
INFO Training on window [0:286], testing on window [286:338]
INFO step 0 loss = 1.01131
INFO step 1000 loss = -0.242592
INFO Training on window [0:312], testing on window [312:364]
INFO step 0 loss = 0.983859
INFO step 1000 loss = -0.279851
INFO Training on window [0:338], testing on window [338:390]
INFO step 0 loss = 0.560554
INFO step 1000 loss = -0.209488
INFO Training on window [0:364], testing on window [364:416]
INFO step 0 loss = 0.716816
INFO step 1000 loss = -0.369162
INFO Training on window [0:390], testing on window [390:442]
INFO step 0 loss = 0.391474
INFO step 1000 loss = -0.45527
INFO Training on window [0:416], testing on window [416:468]
INFO step 0 loss = 0.37326
INFO step 1000 loss = -0.508014
CPU times: user 4min 1s, sys: 960 ms, total: 4min 2s
Wall time: 4min 2s
[22]:
fig, axes = plt.subplots(3, figsize=(8, 6), sharex=True)
axes[0].set_title("Gaussian versus Stable accuracy over {} windows".format(len(windows2)))
axes[0].plot([w["crps"] for w in windows2], "b<", label="Gaussian")
axes[0].plot([w["crps"] for w in windows3], "r>", label="Stable")
axes[0].set_ylabel("CRPS")
axes[1].plot([w["mae"] for w in windows2], "b<", label="Gaussian")
axes[1].plot([w["mae"] for w in windows3], "r>", label="Stable")
axes[1].set_ylabel("MAE")
axes[2].plot([w["rmse"] for w in windows2], "b<", label="Gaussian")
axes[2].plot([w["rmse"] for w in windows3], "r>", label="Stable")
axes[2].set_ylabel("RMSE")
axes[0].legend(loc="best")
plt.tight_layout()
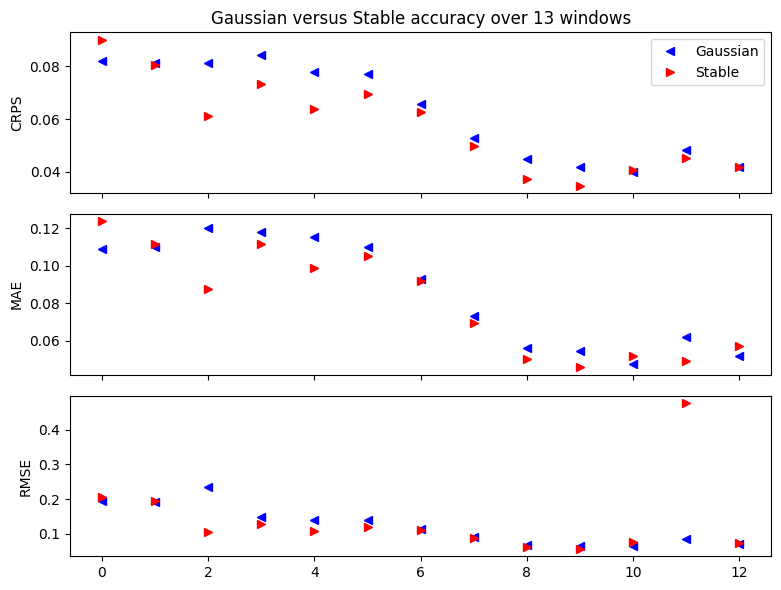
Note that RMSE is a poor metric for evaluating heavy-tailed data. Our stable model has such heavy tails that its variance is infinite, so we cannot expect RMSE to converge, hence occasional outlying points.
[ ]: