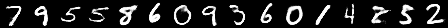Variational Autoencoder with a Normalizing Flow prior

Using a normalizing flow as prior for the latent variables instead of the typical standard Gaussian is an easy way to make a variational autoencoder (VAE) more expressive. This notebook demonstrates how to implement a VAE with a normalizing flow as prior for the MNIST dataset. We strongly recommend to read Pyro’s VAE tutorial first.

In this notebook we use Zuko to implement normalizing flows, but similar results can be obtained with other PyTorch-based flow libraries.

import pyro
import torch
import torch.nn as nn
import torch.utils.data as data
import zuko

from pyro.contrib.zuko import ZukoToPyro
from pyro.optim import Adam
from pyro.infer import SVI, Trace_ELBO
from torch import Tensor
from torchvision.datasets import MNIST
from torchvision.transforms.functional import to_tensor, to_pil_image
from tqdm import tqdm

Data

The MNIST dataset consists of 28 x 28 grayscale images representing handwritten digits (0 to 9).

trainset = MNIST(root='', download=True, train=True, transform=to_tensor)
trainloader = data.DataLoader(trainset, batch_size=256, shuffle=True)

x = [trainset[i][0] for i in range(16)]
x = torch.cat(x, dim=-1)

to_pil_image(x)

Model

As for the previous tutorial, we choose a (diagonal) Gaussian model as encoder \(q_\psi(z | x)\) and a Bernoulli model as decoder \(p_\phi(x | z)\).

class GaussianEncoder(nn.Module):
    def __init__(self, features: int, latent: int):
        super().__init__()

        self.hyper = nn.Sequential(
            nn.Linear(features, 1024),
            nn.ReLU(),
            nn.Linear(1024, 1024),
            nn.ReLU(),
            nn.Linear(1024, 2 * latent),
        )

    def forward(self, x: Tensor):
        phi = self.hyper(x)
        mu, log_sigma = phi.chunk(2, dim=-1)

        return pyro.distributions.Normal(mu, log_sigma.exp()).to_event(1)


class BernoulliDecoder(nn.Module):
    def __init__(self, features: int, latent: int):
        super().__init__()

        self.hyper = nn.Sequential(
            nn.Linear(latent, 1024),
            nn.ReLU(),
            nn.Linear(1024, 1024),
            nn.ReLU(),
            nn.Linear(1024, features),
        )

    def forward(self, z: Tensor):
        phi = self.hyper(z)
        rho = torch.sigmoid(phi)

        return pyro.distributions.Bernoulli(rho).to_event(1)

However, we choose a masked autoregressive flow (MAF) as prior \(p_\phi(z)\) instead of the typical standard Gaussian \(\mathcal{N}(0, I)\). Instead of implementing the MAF ourselves, we borrow it from the Zuko library. Because Zuko distributions are very similar to Pyro distributions, a thin wrapper (ZukoToPyro) is sufficient to make Zuko and Pyro 100% compatible.

class VAE(nn.Module):
    def __init__(self, features: int, latent: int = 16):
        super().__init__()

        self.encoder = GaussianEncoder(features, latent)
        self.decoder = BernoulliDecoder(features, latent)

        self.prior = zuko.flows.MAF(
            features=latent,
            transforms=3,
            hidden_features=(256, 256),
        )

    def model(self, x: Tensor):
        pyro.module("prior", self.prior)
        pyro.module("decoder", self.decoder)

        with pyro.plate("batch", len(x)):
            z = pyro.sample("z", ZukoToPyro(self.prior()))
            x = pyro.sample("x", self.decoder(z), obs=x)

    def guide(self, x: Tensor):
        pyro.module("encoder", self.encoder)

        with pyro.plate("batch", len(x)):
            z = pyro.sample("z", self.encoder(x))

vae = VAE(784, 16).cuda()
vae

VAE(
  (encoder): GaussianEncoder(
    (hyper): Sequential(
      (0): Linear(in_features=784, out_features=1024, bias=True)
      (1): ReLU()
      (2): Linear(in_features=1024, out_features=1024, bias=True)
      (3): ReLU()
      (4): Linear(in_features=1024, out_features=32, bias=True)
    )
  )
  (decoder): BernoulliDecoder(
    (hyper): Sequential(
      (0): Linear(in_features=16, out_features=1024, bias=True)
      (1): ReLU()
      (2): Linear(in_features=1024, out_features=1024, bias=True)
      (3): ReLU()
      (4): Linear(in_features=1024, out_features=784, bias=True)
    )
  )
  (prior): MAF(
    (transform): LazyComposedTransform(
      (0): MaskedAutoregressiveTransform(
        (base): MonotonicAffineTransform()
        (order): [0, 1, 2, 3, 4, ..., 11, 12, 13, 14, 15]
        (hyper): MaskedMLP(
          (0): MaskedLinear(in_features=16, out_features=256, bias=True)
          (1): ReLU()
          (2): MaskedLinear(in_features=256, out_features=256, bias=True)
          (3): ReLU()
          (4): MaskedLinear(in_features=256, out_features=32, bias=True)
        )
      )
      (1): MaskedAutoregressiveTransform(
        (base): MonotonicAffineTransform()
        (order): [15, 14, 13, 12, 11, ..., 4, 3, 2, 1, 0]
        (hyper): MaskedMLP(
          (0): MaskedLinear(in_features=16, out_features=256, bias=True)
          (1): ReLU()
          (2): MaskedLinear(in_features=256, out_features=256, bias=True)
          (3): ReLU()
          (4): MaskedLinear(in_features=256, out_features=32, bias=True)
        )
      )
      (2): MaskedAutoregressiveTransform(
        (base): MonotonicAffineTransform()
        (order): [0, 1, 2, 3, 4, ..., 11, 12, 13, 14, 15]
        (hyper): MaskedMLP(
          (0): MaskedLinear(in_features=16, out_features=256, bias=True)
          (1): ReLU()
          (2): MaskedLinear(in_features=256, out_features=256, bias=True)
          (3): ReLU()
          (4): MaskedLinear(in_features=256, out_features=32, bias=True)
        )
      )
    )
    (base): Unconditional(DiagNormal(loc: torch.Size([16]), scale: torch.Size([16])))
  )
)

Training

We train our VAE with a standard stochastic variational inference (SVI) pipeline.

pyro.clear_param_store()

svi = SVI(vae.model, vae.guide, Adam({'lr': 1e-3}), loss=Trace_ELBO())

for epoch in (bar := tqdm(range(96))):
    losses = []

    for x, _ in trainloader:
        x = x.round().flatten(-3).cuda()

        losses.append(svi.step(x))

    losses = torch.tensor(losses)

    bar.set_postfix(loss=losses.sum().item() / len(trainset))

100%|██████████| 96/96 [24:04<00:00, 15.05s/it, loss=63.1]

After training, we can generate MNIST images by sampling latent variables from the prior and decoding them.

z = vae.prior().sample((16,))
x = vae.decoder(z).mean.reshape(-1, 28, 28)

to_pil_image(x.movedim(0, 1).reshape(28, -1))