Understanding Hyperbole using RSA¶
"My new kettle cost a million dollars."
Hyperbole – using an exagerated utterance to convey strong opinions – is a common non-literal use of language. Yet non-literal uses of langauge are impossible under the simplest RSA model. Kao, et al, suggested that two ingredients could be added to ennable RSA to capture hyperbole. First, the state conveyed by the speaker and reasoned about by the listener should include affective dimensions. Second, the speaker only intends to convey information relevant to a particular topic, such as “how expensive was it?” or “how am I feeling about the price?”; pragmatic listeners hence jointly reason about this topic and the state.
[1]:
#first some imports
import torch
torch.set_default_dtype(torch.float64) # double precision for numerical stability
import collections
import argparse
import matplotlib.pyplot as plt
import pyro
import pyro.distributions as dist
import pyro.poutine as poutine
from search_inference import HashingMarginal, memoize, Search
As in the simple RSA example, the inferece helper Marginal takes an un-normalized stochastic function, constructs the distribution over execution traces by using Search, and constructs the marginal distribution on return values (via HashingMarginal).
[2]:
def Marginal(fn):
return memoize(lambda *args: HashingMarginal(Search(fn).run(*args)))
The domain for this example will be states consisting of price (e.g. of a tea kettle) and the speaker’s emotional arousal (whether the speaker thinks this price is irritatingly expensive). Priors here are adapted from experimental data.
[3]:
State = collections.namedtuple("State", ["price", "arousal"])
def price_prior():
values = [50, 51, 500, 501, 1000, 1001, 5000, 5001, 10000, 10001]
probs = torch.tensor([0.4205, 0.3865, 0.0533, 0.0538, 0.0223, 0.0211, 0.0112, 0.0111, 0.0083, 0.0120])
ix = pyro.sample("price", dist.Categorical(probs=probs))
return values[ix]
def arousal_prior(price):
probs = {
50: 0.3173,
51: 0.3173,
500: 0.7920,
501: 0.7920,
1000: 0.8933,
1001: 0.8933,
5000: 0.9524,
5001: 0.9524,
10000: 0.9864,
10001: 0.9864
}
return pyro.sample("arousal", dist.Bernoulli(probs=probs[price])).item() == 1
def state_prior():
price = price_prior()
state = State(price=price, arousal=arousal_prior(price))
return state
Now we define a version of the RSA speaker that only produces relevant information for the literal listener. We define relevance with respect to a Question Under Discussion (QUD) – this can be thought of as defining the speaker’s current attention or topic.
The speaker is defined mathematically by:
To implement this as a probabilistic program, we start with a helper function project, which takes a distribution over some (discrete) domain and a function qud on this domain. It creates the push-forward distribution, using Marginal (as a Python decorator). The speaker’s relevant information is then simply information about the state in this projection.
[4]:
@Marginal
def project(dist,qud):
v = pyro.sample("proj",dist)
return qud_fns[qud](v)
@Marginal
def literal_listener(utterance):
state=state_prior()
pyro.factor("literal_meaning", 0. if meaning(utterance, state.price) else -999999.)
return state
@Marginal
def speaker(state, qud):
alpha = 1.
qudValue = qud_fns[qud](state)
with poutine.scale(scale=torch.tensor(alpha)):
utterance = utterance_prior()
literal_marginal = literal_listener(utterance)
projected_literal = project(literal_marginal, qud)
pyro.sample("listener", projected_literal, obs=qudValue)
return utterance
The possible QUDs capture that the speaker may be attending to the price, her affect, or some combination of these. We assume a uniform QUD prior.
[5]:
#The QUD functions we consider:
qud_fns = {
"price": lambda state: State(price=state.price, arousal=None),
"arousal": lambda state: State(price=None, arousal=state.arousal),
"priceArousal": lambda state: State(price=state.price, arousal=state.arousal),
}
def qud_prior():
values = list(qud_fns.keys())
ix = pyro.sample("qud", dist.Categorical(probs=torch.ones(len(values)) / len(values)))
return values[ix]
Now we specify the utterance meanings (standard number word denotations: “N” means exactly \(N\)) and a uniform utterance prior.
[6]:
def utterance_prior():
utterances = [50, 51, 500, 501, 1000, 1001, 5000, 5001, 10000, 10001]
ix = pyro.sample("utterance", dist.Categorical(probs=torch.ones(len(utterances)) / len(utterances)))
return utterances[ix]
def meaning(utterance, price):
return utterance == price
OK, let’s see what number term this speaker will say to express different states and QUDs.
[7]:
#silly plotting helper:
def plot_dist(d):
support = d.enumerate_support()
data = [d.log_prob(s).exp().item() for s in d.enumerate_support()]
names = support
ax = plt.subplot(111)
width=0.3
bins = list(map(lambda x: x-width/2,range(1,len(data)+1)))
ax.bar(bins,data,width=width)
ax.set_xticks(list(map(lambda x: x, range(1,len(data)+1))))
ax.set_xticklabels(names,rotation=45, rotation_mode="anchor", ha="right")
# plot_dist( speaker(State(price=50, arousal=False), "arousal") )
# plot_dist( speaker(State(price=50, arousal=True), "price") )
plot_dist( speaker(State(price=50, arousal=True), "arousal") )
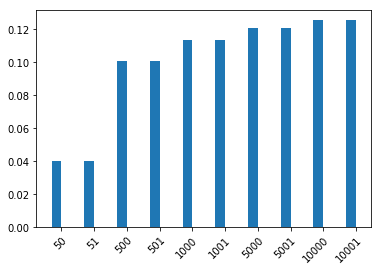
Try different values above! When will the speaker favor non-literal utterances?
Finally, the pragmatic listener doesn’t know what the QUD is and so jointly reasons abut this and the state.
[8]:
@Marginal
def pragmatic_listener(utterance):
state = state_prior()
qud = qud_prior()
speaker_marginal = speaker(state, qud)
pyro.sample("speaker", speaker_marginal, obs=utterance)
return state
How does this listener interpret the uttered price “10,000”? On the one hand this is a very unlikely price a priori, on the other if it were true it would come with strong arousal. Altogether this becomes a plausible hyperbolic utterence:
[9]:
plot_dist( pragmatic_listener(10000) )
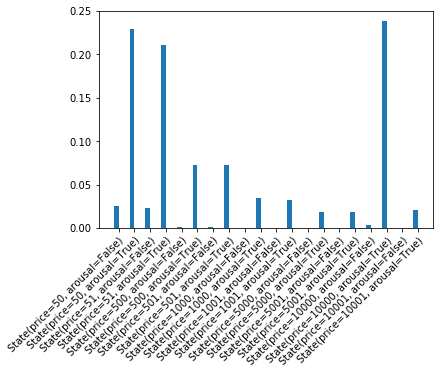
Pragmatic Halo¶
“It cost fifty dollars” is often interpretted as costing around 50 – plausibly 51; yet “it cost fiftyone dollars” is interpretted as 51 and definitely not 50. This assymetric imprecision is often called the pragmatic halo or pragmatic slack.
We can extend the hyperole model to capture this additional non-literal use of numbers by including QUD functions that collapse nearby numbers and assuming that round numbers are slightly more likely (because they are less difficult to utter).
[10]:
#A helper to round a number to the nearest ten:
def approx(x, b=None):
if b is None:
b = 10.
div = float(x)/b
rounded = int(div) + 1 if div - float(int(div)) >= 0.5 else int(div)
return int(b) * rounded
#The QUD functions we consider:
qud_fns = {
"price": lambda state: State(price=state.price, arousal=None),
"arousal": lambda state: State(price=None, arousal=state.arousal),
"priceArousal": lambda state: State(price=state.price, arousal=state.arousal),
"approxPrice": lambda state: State(price=approx(state.price), arousal=None),
"approxPriceArousal": lambda state: State(price=approx(state.price), arousal=state.arousal),
}
def qud_prior():
values = list(qud_fns.keys())
ix = pyro.sample("qud", dist.Categorical(probs=torch.ones(len(values)) / len(values)))
return values[ix]
def utterance_cost(numberUtt):
preciseNumberCost = 10.
return 0. if approx(numberUtt) == numberUtt else preciseNumberCost
def utterance_prior():
utterances = [50, 51, 500, 501, 1000, 1001, 5000, 5001, 10000, 10001]
utteranceLogits = -torch.tensor(list(map(utterance_cost, utterances)),
dtype=torch.float64)
ix = pyro.sample("utterance", dist.Categorical(logits=utteranceLogits))
return utterances[ix]
The RSA speaker and listener definitions are unchanged:
[11]:
@Marginal
def literal_listener(utterance):
state=state_prior()
pyro.factor("literal_meaning", 0. if meaning(utterance, state.price) else -999999.)
return state
@Marginal
def speaker(state, qud):
alpha = 1.
qudValue = qud_fns[qud](state)
with poutine.scale(scale=torch.tensor(alpha)):
utterance = utterance_prior()
literal_marginal = literal_listener(utterance)
projected_literal = project(literal_marginal, qud)
pyro.sample("listener", projected_literal, obs=qudValue)
return utterance
@Marginal
def pragmatic_listener(utterance):
state = state_prior()
qud = qud_prior()
speaker_marginal = speaker(state, qud)
pyro.sample("speaker", speaker_marginal, obs=utterance)
return state
OK, let’s see if we get the desired assymetric slack (we’re only interested in the interpretted price here, so we marginalize out the arousal).
[12]:
@Marginal
def pragmatic_listener_price_marginal(utterance):
return pyro.sample("pm", pragmatic_listener(utterance)).price
plot_dist(pragmatic_listener_price_marginal(50))
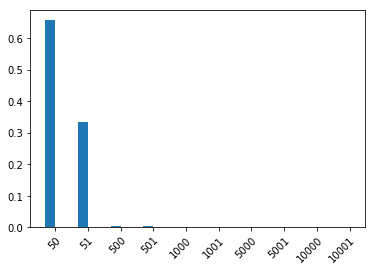
[13]:
plot_dist(pragmatic_listener_price_marginal(51))

Irony and More Complex Affect¶
In the above hyperbole model we assumed a very simple model of affect: a single dimension with two values (high and low arousal). Actual affect is best represented as a two-dimensional space corresponding to valence and arousal. Kao and Goodman (2015) showed that extending the affect space to these two dimensions immediately introduces a new usage of numbers: verbal irony in which an utterance corresponding to a high-arousal positive valence state is used to convey a high-arousal but negative valence (or vice versa).