SVI with a Normalizing Flow guide¶
Thanks to their expressiveness, normalizing flows (see normalizing flow introduction) are great guide candidates for stochastic variational inference (SVI). This notebook demonstrates how to perform amortized SVI with a normalizing flow as guide.
In this notebook we use Zuko to implement normalizing flows, but similar results can be obtained with other PyTorch-based flow libraries.
[1]:
import pyro
import torch
import zuko # pip install zuko
from corner import corner, overplot_points # pip install corner
from pyro.contrib.zuko import ZukoToPyro
from pyro.optim import ClippedAdam
from pyro.infer import SVI, Trace_ELBO
from torch import Tensor
Model¶
We define a simple non-linear model \(p(x | z)\) with a standard Gaussian prior \(p(z)\) over the latent variables \(z\).
[2]:
prior = pyro.distributions.Normal(torch.zeros(3), torch.ones(3)).to_event(1)
def likelihood(z: Tensor):
mu = z[..., :2]
rho = z[..., 2].tanh() * 0.99
cov = 1e-2 * torch.stack([
torch.ones_like(rho), rho,
rho, torch.ones_like(rho),
], dim=-1).unflatten(-1, (2, 2))
return pyro.distributions.MultivariateNormal(mu, cov)
def model(x: Tensor):
with pyro.plate("data", x.shape[1]):
z = pyro.sample("z", prior)
with pyro.plate("obs", 5):
pyro.sample("x", likelihood(z), obs=x)
We sample 64 reference latent variables and observations \((z^*, x^*)\). In practice, \(z^*\) is unknown, and \(x^*\) is your data.
[3]:
z_star = prior.sample((64,))
x_star = likelihood(z_star).sample((5,))
Guide¶
We define the guide \(q_\phi(z | x)\) with a normalizing flow. We choose a conditional neural spline flow borrowed from the Zuko library. Because Zuko distributions are very similar to Pyro distributions, a thin wrapper (ZukoToPyro) is sufficient to make Zuko and Pyro 100% compatible.
[4]:
flow = zuko.flows.NSF(features=3, context=10, transforms=1, hidden_features=(256, 256))
flow.transform = flow.transform.inv # inverse autoregressive flow (IAF) are fast to sample from
def guide(x: Tensor):
pyro.module("flow", flow)
with pyro.plate("data", x.shape[1]): # amortized
pyro.sample("z", ZukoToPyro(flow(x.transpose(0, 1).flatten(-2))))
SVI¶
We train our guide with a standard stochastic variational inference (SVI) pipeline. We use 16 particles to reduce the variance of the ELBO and clip the norm of the gradients to make training more stable.
[5]:
pyro.clear_param_store()
svi = SVI(model, guide, optim=ClippedAdam({"lr": 1e-3, "clip_norm": 10.0}), loss=Trace_ELBO(num_particles=16, vectorize_particles=True))
for step in range(4096 + 1):
elbo = svi.step(x_star)
if step % 256 == 0:
print(f'({step})', elbo)
(0) 209195.08367919922
(256) -25.225540161132812
(512) -99.09033203125
(768) -102.66302490234375
(1024) -138.8058319091797
(1280) -92.15625
(1536) -136.78167724609375
(1792) -87.76119995117188
(2048) -116.21714782714844
(2304) -162.0266571044922
(2560) -91.13175964355469
(2816) -164.86270141601562
(3072) -98.17607116699219
(3328) -102.58432006835938
(3584) -151.61912536621094
(3840) -77.94436645507812
(4096) -121.82719421386719
Posterior predictive¶
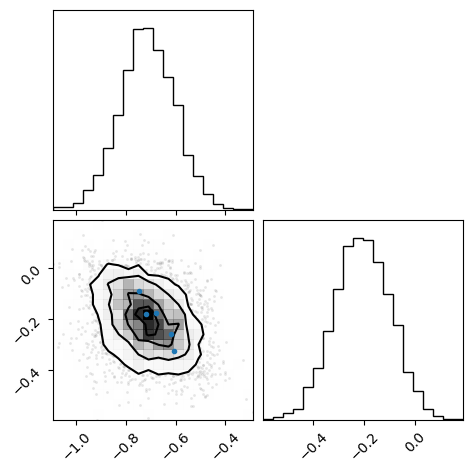
[6]:
z = flow(x_star[:, 0].flatten()).sample((4096,))
x = likelihood(z).sample()
fig = corner(x.numpy())
overplot_points(fig, x_star[:, 0].numpy())
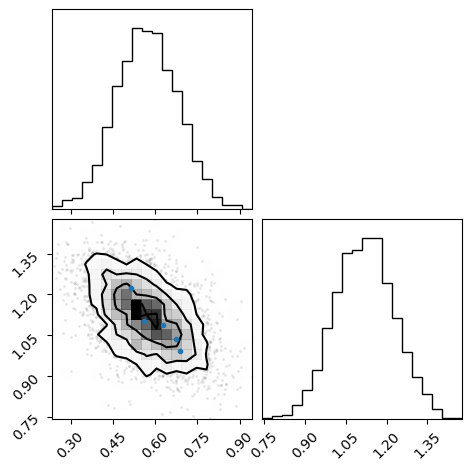
[7]:
z = flow(x_star[:, 1].flatten()).sample((4096,))
x = likelihood(z).sample()
fig = corner(x.numpy())
overplot_points(fig, x_star[:, 1].numpy())